

For each input symbol, the state to which the machine will move can be determined using DFA. Meanwhile, the power of these new automata is exactly the same as the automata we already had, so we don't seem to have gained anything. A deterministic finite automaton (DFA) is a finite-state machine that accepts or rejects a given string of symbols by running through a state sequence that is uniquely determined by the string in the theory of computation. But the fact that the $\varepsilon$-transitions introduce nondeterminism means that it'll be harder to analyze what's going on. This new type of automaton seems to combine the disadvantages of both: requiring exactly one transition per state per symbol and at most one $\varepsilon$-transition per state means that it's still going to be fiddly to design an automaton that does what you want. Conversely, NFAs are quite easy to construct but it can be hard to analyze what they're doing – for example, compare how annoyingly difficult it is to precisely define the language accepted by an NFA, compared to a DFA. So, what have we achieved? The advantage of DFAs is that they're easy to analyze but it can be hard to construct a DFA to accept a particular language – if you don't believe me, design an algorithm that converts arbitrary regular expressions straight to DFAs, without using NFAs as an intermediate stage. And any DFA is just one of these automata where $\delta(q,\varepsilon)=q$ for every state $q$, so every regular language is accepted by an automaton of this kind.
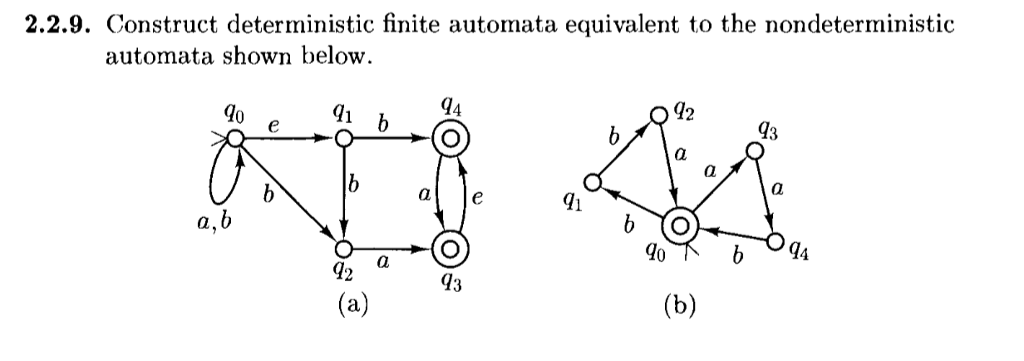
It's a special kind of NFA, so it can't accept any non-regular language. We can also see that this new type of automaton accepts exactly the regular languages. First, note that, if you don't want a $\varepsilon$-transition from some particular state, you can set $\delta(q,\varepsilon)=q$. Let's briefly investigate the properties of such a machine. For each state, there's also a state the automaton can move to without reading a character of input (this is $\delta(q,\varepsilon)$). That is, for each state $q$ and each symbol $a$ in the alphabet, there's exactly one state that the automaton moves to after reading that symbol. I guess the definition you have in mind is that the transition function has the form $\delta\colon Q\times (\Sigma\cup\)\to Q$. DFA is used in Lexical Analysis in Compiler.Expanding on adrianN's comment, sure, you can define one if you want but what would be the point?.There can be multiple final states in both NFA and DFA.
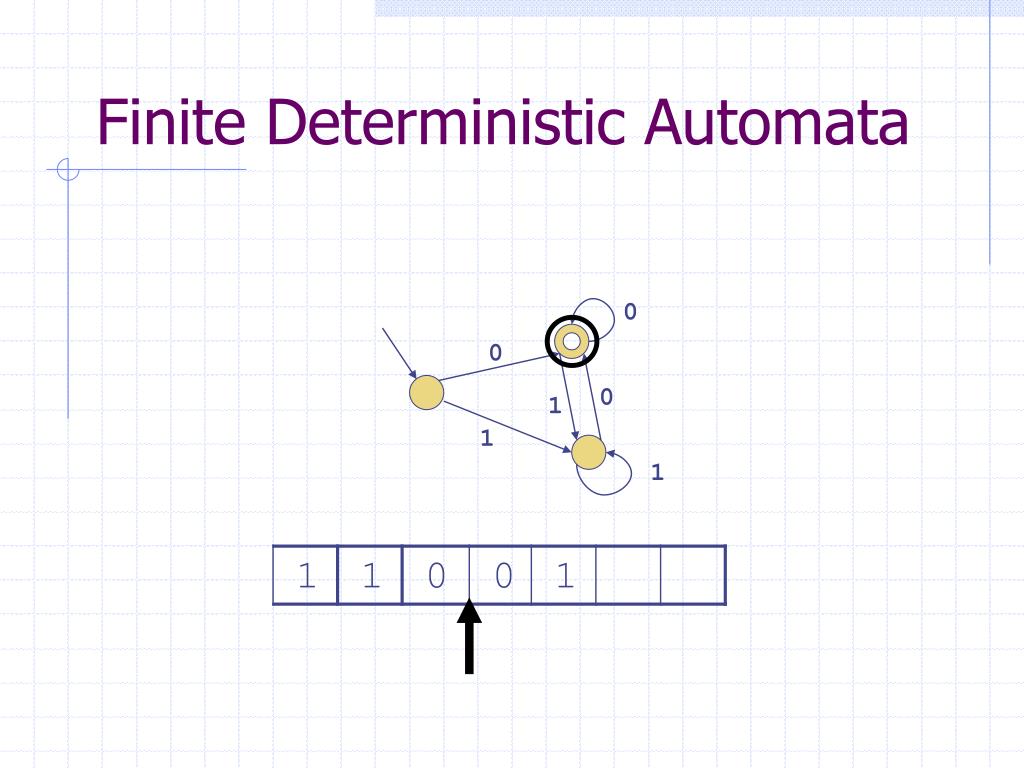
It is used to transmit any number of states for a particular input. NFA stands for non-deterministic finite automata. (Informal) A deterministic finite automaton1 (DFA) con. In the DFA, the machine goes to one state only for a particular input character. We now want to construct a machine, an automaton, for this language. Deterministic refers to the uniqueness of the computation. In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if each of its transitions is uniquely determined by its source state and input symbol, and reading an input symbol is required for each state transition. Types of Automata:ĭFA refers to deterministic finite automata. The tape reader reads the cells one by one from left to right, and at a time only one input symbol is read. Each input symbol is placed in each cell.įinite control: The finite control decides the next state on receiving particular input from input tape. Input tape: It is a linear tape having some number of cells. Finite automata can be represented by input tape and finite control.


 0 kommentar(er)
0 kommentar(er)
